codetop 100 题(暂定)思路笔记
两数之和
题目条件说答案唯一,hash 表存 target-x 即可。
时间:,空间:
三数之和
基本思路是遍历数组对每个值求两数之和,易知时间复杂度必为。
题目要求答案不可重复,但是数组中会出现重复值,如[1,2,-3,2],使用 hash 表扫一遍还要去重,所以不使用 hash 表。
因此先排序,再使用双指针从两端遍历,双指针可以跳过重复的值。
时间:+=,空间:
四数之和 I
四数之和 II
最大连续子序(子数组)和
给你一个整数数组 nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
DP
DP 最优,遍历一遍,直观理解是当前序列之和<0 就可以从下一个大于 0 的元素开始继续遍历,转移方程为:
时间:,空间:
线段树
区间求和就用线段树喵~线段树可以求任意区间最大和,存了其他区间信息所以空间复杂度会高一点。
时间:,空间:
乘积最大子数组
联系 最大子序和 一起看。
本题中由于存在负数相乘得正,因此单纯用一维 DP 保存 nums[i]前的 max 是做不到状态转移的,而易知 max 正数*负数=min,因此考虑使用二维 DP 保存 max 和 min。
时间:,空间:
最长回文子串
典中典 DP,从下到上,从左到右,遍历上三角状态转移矩阵。
时间:,空间:,也可以不存具体矩阵,从状态[i,i]往右上角一路转移,这时空间:。
Manacher 算法可以达到的时空复杂度,不看。
搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。
例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target,如果 nums 中存在这个目标值 target,则返回它的下标,否则返回 -1。
二叉查找
时间:,空间:
搜索二维矩阵 II
搜索二维矩阵 I 用两次二分查找就行,而 II 不行,因为此题的行与行之间都有区间重叠。有一个小 trick:
抽象 BST
将矩阵看作以 matrix[0][m-1] 为 root 的 BST。
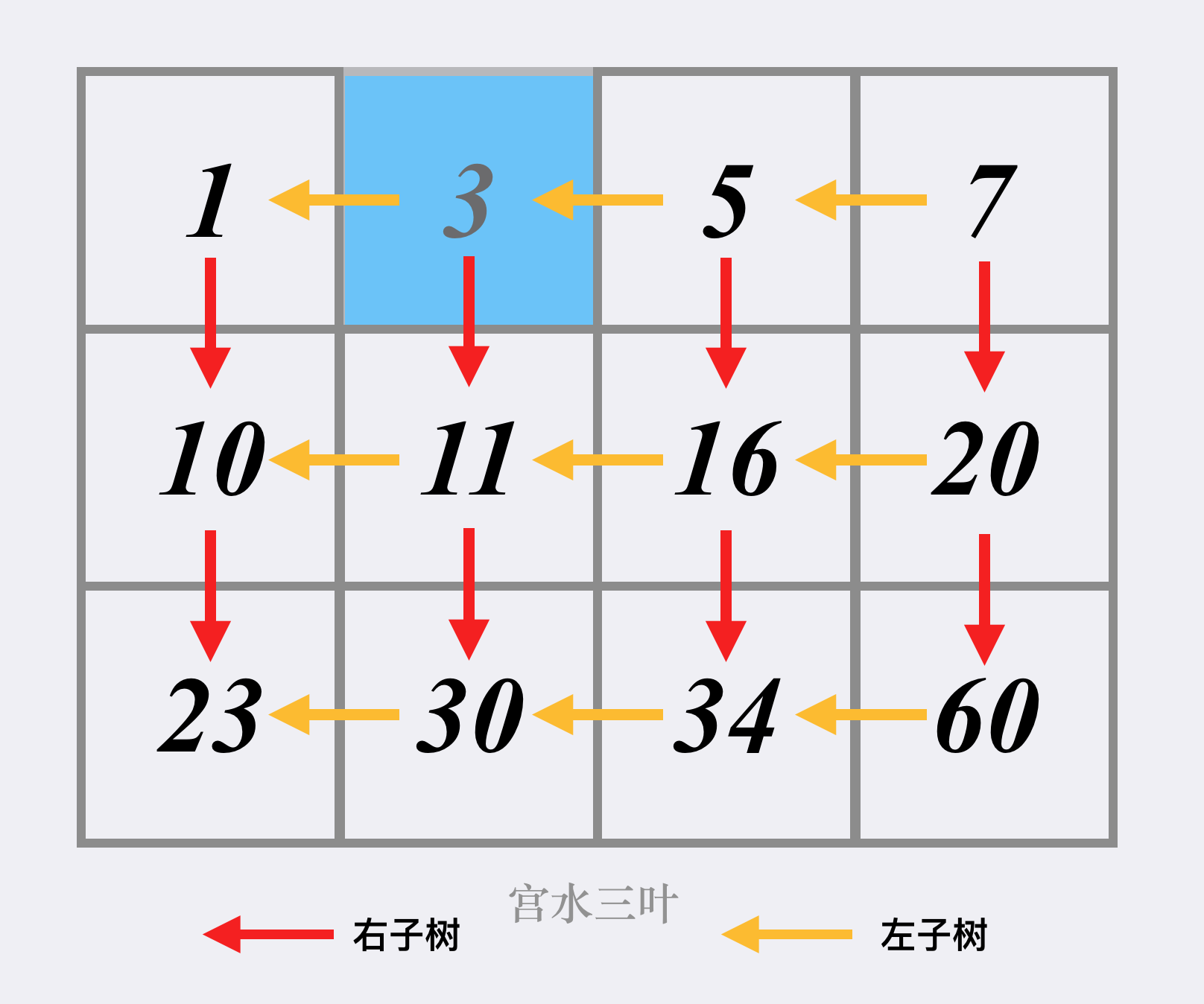
那么问题就简单了
-
如果 matrix[x,y]==target,说明搜索完成;
-
如果 matrix[x,y]>target,由于每一列的元素都是升序排列的,那么在当前的搜索矩阵中,所有位于第 y 列的元素都是严格大于 target 的,因此我们可以将它们全部忽略,即将 y 减少 1;
-
如果 matrix[x,y]<target,由于每一行的元素都是升序排列的,那么在当前的搜索矩阵中,所有位于第 x 行的元素都是严格小于 target 的,因此我们可以将它们全部忽略,即将 x 增加 1。
时间:,空间:
检测环形链表 I+II
快慢指针,快指针一次两格,慢指针一次一格。若快慢指针相遇了则链表有环。
经过数学计算,用另两个指针从快慢指针相遇节点和头节点同时前进,最终相遇的节点为环入口。
时间:,空间:
缺失的第一个正数
最优解为时间:,空间:
这里需要记得长度为 N 的 nums 缺失的第一个正数一定 。
置换
将 处的 nums[i] 置换到 nums[i]-1 处去,一直换到 或者不 。
这里不能是 ,这样会导致出现重复正数时死循环,即 但 。最后再遍历一下数组看看哪个 即可。
原数组当哈希表
由于不可使用额外哈希表来存,所以更改原数组。
本题的哈希表只起到标记作用,所以更接近位图的用法。寻找的又是正数,所以当 nums[i]=4,将 nums[4]处的数据改成-nums[4]就可以标记了。
遍历一遍后,不是负数的 nums[i]就代表正数没出现过。
这样标记有一个前提要满足,就是数组里全是正数。而易知,所以可以先遍历一遍数组把所有负数都改成 N+1。
然后可以得到全都是正数的 nums,再遍历一遍,取 nums[i]元素时加个 abs() 就可以了。
时间:,空间:
寻找重复数
对照缺失的第一个正数。本题不允许修改数组,否则按置换法,当 并且 时,nums[i]显然就是重复数。
这里就要想到将 i 看作 i->nums[i]的边(不能和缺失的第一个正数一样 i->nums[i]-1,因为 nums[0]没有入度这一点很重要),则重复数将指向同一个 nums[i],图中一定有环。给出证明:
- 首先考虑一个长度为 N 的数组,里面存的都是不重复的的数,按 nums[i]->nums[nums[i]] 这样的连线规则,我们可以想到 nums[0]没有入度,而 nums[N]不存在,可以当作终点。
- 我们可以证明一个元素要么处于一个环中,要么不处于环中。
- 其次必然存在一条从 nums[0]->…->nums[N]的路。这要用到 nums[0]没有入度这一点,假如从 nums[0]出发却陷入环,因为nums[0]必然不处于环中,因此 nums[0]和某个 nums[j]是相等的,而这是不可能的。从 nums[0]出发的路必然不会陷入环中,那么就必然能跳出去,而跳出去的唯一终止条件就是 nums[N],因此得证。
- 再考虑一个长度为 N+1 的数组。这时不仅 nums[N]有映射了,而且,这显然意味着终点已经不存在了,从 nums[0]出发必然到达 nums[N],而 nums[N]只会跳回去,因此这个数组一定存在环,而这个环的入口就是重复数。
- 这里同样可以思考为什么从 nums[0]出发找到的那个环的入口就一定是重复数,毕竟数组还有很多其他的环。答案也很简单,仍然是nums[0]必然不处于环中,后续推理与 nums[0]->…->nums[N]一致。
证明了从 nums[i]出发存在环,那么检测方法就等价于 检测环形链表 。
时间:,空间:
岛屿数量
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
BFS|DFS|并查集
时间:,空间:,BFS 空间为 O(min(M,N))
LCA(最近公共祖先)树
递归
一次查询用递归,原理就是从 root 开始,只要出现一边存在 p 一边存在 q 的情况,那这个节点就是 LCA 了。
时间:,空间:
倍增法
多次查询就可以记录子节点的父节点了,这里有两个过程可以通过倍增法加速。首先是将较深的节点提升到和较浅的节点一样深,然后是直接找两者的 LCA。
倍增法核心在于要使用保留子节点的个父节点,然后直接从最大的那个父节点开始往小搜索。这里充分利用了相加可以逼近任意正数的特性,比如 13=8+4+1。
时间:建立后,单次搜索,空间:
和为 K 的子数组
前缀和
时间:,空间:
路径总和 III
给定一个二叉树的根节点 root,和一个整数 targetSum,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
前缀和
从 root 往下遍历的时候使用前缀和和一个哈希表,也就是 两数之和 的方法就行。因为前缀和 j-前缀和 i=[i,j]的路径总和,参考 和为 K 的子数组。
时间:,空间:
2D 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
对于下标 i,下雨后水能到达的最大高度等于下标 i 两边的最大高度的最小值,下标 i 处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i]。
DP
预处理获得两个数组 leftmax 和 rightmax,对于 ,下标 处能接的雨水量等于
时间:,空间:
单调栈
时间:,空间:
双指针
时间:,空间:
柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
这道题主要在于遍历的方式,我们可以轻松想到最暴力的方法,对每一个元素的高都遍历一遍数组看看能有多长,面积有多大。
这时可以发现,并不需要每次都从头开始遍历,参考接雨水,从当前元素往两边延伸,找到第一个小于自己的元素即可,也就是两个数组,左边第一个小于自己的,右边第一个小于自己的,两者相减就是长,当前元素负责的最大的矩形面积就可以得出。这种找到第一个大/小于自己的元素显然使用单调栈。
单调栈
时间:,空间:
螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix,请按照 顺时针螺旋顺序,返回矩阵中的所有元素。
按层(圈)模拟,可以将矩阵看成若干层,首先输出最外层的元素,其次输出次外层的元素,直到输出最内层的元素。
时间:,空间:
螺旋矩阵 II
给你一个正整数 n,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix。
还是绕圈圈。
时间:,空间:
相交链表
给你两个单链表的头节点 headA 和 headB,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null。
双指针,a 指针遍历完 headA 遍历 headB,b 指针遍历完 headB 遍历 headA,两者遍历长度相等,最终会相遇在相交节点处。没相遇就是没相交。
时间:,空间:
假如链表可能存在环呢?
当处理可能包含环的链表,并寻找它们相交的节点时,问题变得复杂。以下是几种不同的解法思路:
方法 1:使用哈希集合
- 遍历第一个链表,并将所有节点存储在一个哈希集合中。
- 遍历第二个链表,检查每个节点是否存在于哈希集合中。如果存在,则该节点是相交点。
这种方法简单直接,时间复杂度为 O(N+M),空间复杂度为 O(N) 或 O(M),其中 N 和 M 分别是两个链表的长度。
方法 2:检测环并找到入环节点
- 首先,分别对两个链表进行环检测(Floyd 判圈算法)。如果一个链表有环而另一个没有,则它们不可能相交。如果都没有环,则退化到无环链表相交的经典问题。
- 如果两个链表都有环,则进一步分析:
- 检查两个链表的环入口是否相同。如果相同,说明两链表在进入环之前就已经相交,此时可以转化为无环链表相交的问题。
- 如果环入口不同,则需要遍历其中一个环,检查是否有任何节点与另一个链表的环入口重合。如果有,则这些节点就是相交点;如果没有,则链表不相交。
最长递增子序列
给你一个整数数组 nums,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
DP
时间:,空间:
贪心 + 二分查找
维护一个长得像单调栈的数组 d,但注意不能按单调栈来做,因为比如 [2,3,4] 遇到 1 会 pop 掉所有的元素,但要是后面还有个 5,那就错了。
d[i]表示长度为 i 的所有子序列末尾元素最小的。每一步都将当前值插入 d 数组,将由于 d 本身递增,所以可以使用二分查找达到 logN 的插入效率。
以输入序列 [90,100,1,101,102]为例:
- 第一步插入 90,d=[90];
- 第二步插入 100,d=[90,100];
- 第三步插入 1,d=[1,100];
- 第四步插入 101,d=[1,100,101];
- 第五步插入 102,d=[1,100,101,102]。
再以输入序列 [90,100,1,2,3]为例:
- 第一步插入 90,d=[90];
- 第二步插入 100,d=[90,100];
- 第三步插入 1,d=[1,100];
- 第四步插入 2,d=[1,2];
- 第五步插入 3,d=[1,2,3]。
d 数组并不是最终子序列结果,但是其长度是最长子序列的长。这相当于将所有可能的递增子序列重叠在了一起。
时间:O(NlogN),空间:
合并区间
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠,将它们合并为 [1,6].
按照区间的左端点排序,那么在排完序的列表中,可以合并的区间一定是连续的。
时间:O(NlogN),空间:,空间为排序所需空间
二叉树的直径
二叉搜索树中第 K 小的元素
二叉树中的最大路径和
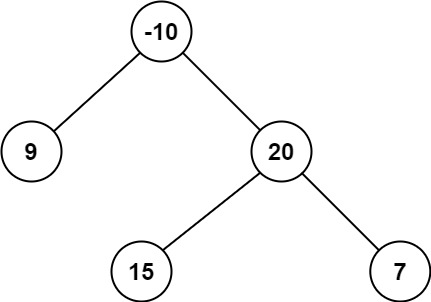
输入:root = [-10,9,20,null,null,15,7]
输出:42
解释:最优路径是 15 -> 20 -> 7,路径和为 15 + 20 + 7 = 42
保存每个节点的最大路径和,即
最大路径和则是
要么是从某个节点往下延伸的一长条,要么是某个节点连着自身两棵子树的组成的三角形(?)。
时间:,空间:
x 的平方根
二分、Newton 迭代
回文链表
快慢指针找中点,分裂成两条链表,反转后半段链表,判断一下,再反转回去。
时间:,空间:
重排链表
给定一个单链表 L 的头节点 head,单链表 L 表示为:
请将其重新排列后变为:
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
与回文链表一致。快慢指针找中点,分裂成两条链表,反转后半段链表,进行交叉合并。
时间:,空间:
排序链表
给你链表的头结点 head,请将其按 升序 排列并返回 排序后的链表。
自底向上归并排序。
时间:O(NlogN),空间:
编辑距离
给你两个单词 word1 和 word2,请返回将 word1 转换成 word2 所使用的最少操作数。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
DP
D[i][j]代表 w1[0…i]和 w2[0…j]的编辑距离。
以 A=horse,B=ros 为例。若 A[i]和 B[j]不等,其更新有以下三种情况:
- 在单词 A 中插入一个字符:如果我们知道 horse 到 ro 的编辑距离为 a,那么显然 horse 到 ros 的编辑距离不会超过 a + 1。这是因为我们可以在 a 次操作后将 horse 和 ro 变为相同的字符串,只需要额外的 1 次操作,在单词 A 的末尾添加字符 s,就能在 a + 1 次操作后将 horse 和 ro 变为相同的字符串;
- 在单词 B 中插入一个字符:如果我们知道 hors 到 ros 的编辑距离为 b,那么显然 horse 到 ros 的编辑距离不会超过 b + 1,原因同上;
- 修改单词 A 的一个字符:如果我们知道 hors 到 ro 的编辑距离为 c,那么显然 horse 到 ros 的编辑距离不会超过 c + 1,原因同上。
那么从 horse 变成 ros 的编辑距离应该为
若 A[i]==B[j],同理推导,则
时间:,空间:,因为 D[i][j]只依赖 左\左上\上 的状态,所以也可以压缩状态矩阵空间为 O(min{M,N})
最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
DP
D[i][j]代表 w1[0…i]和 w2[0…j]的最长公共子序列长度。
D[i][j]=\left\{ \begin{align} & D[i-1][j-1]+1, & test_1[i-1]=text_2[j-1], \\ & max\{D[i-1][j],D[i][j-1]\}, & test_1[i-1]\not =text_2[j-1] \end{align} \right.
时间:,空间:,同 编辑距离 ,只依赖 left\left-top\top 的状态,可压缩为 O(min{M,N})
二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
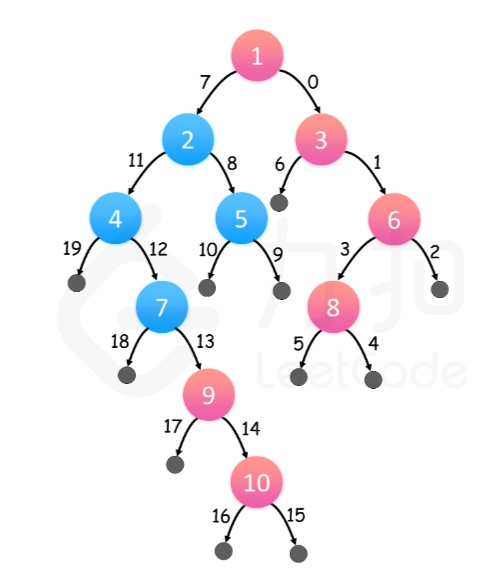
层序遍历即可。
寻找两个正序数组的中位数
需要考虑 nums1=[1,2],nums2=[3,4,5]这种情况。
复原 IP 地址
给定一个只包含数字的字符串 s,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入’.'来形成。你不能重新排序或删除 s 中的任何数字。你可以按任何顺序返回答案。
示例 3:
输入:s = “101023”
输出:[“1.0.10.23”,“1.0.102.3”,“10.1.0.23”,“10.10.2.3”,“101.0.2.3”]
回溯。
滑动窗口最大值
最大堆
时间:O(NlogN),空间:
单调队列
维护一个存着数组下标的单调递减队列。
易知队首是当前滑动窗口最大值,滑一次就拿新元素跟队尾元素比,假如队尾元素小就意味着新元素在这个滑动窗口一直比它大,它不需要存储,直接 pop 掉,如此反复,队列单调递减可证。
每滑一次还要看队首下标越界没有,越界了也 pop 掉。
所以需要双向对列。
时间:,空间:O(k)
分块 + 预处理
时间:,空间:
下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
- 例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
- 例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
- 类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
- 而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums,找出 nums 的下一个排列。必须 原地 修改,只允许使用额外常数空间。
需分两次扫描。找不到规律,嗯背题解罢。
注意到下一个排列总是比当前排列要大,除非该排列已经是最大的排列。我们希望找到一种方法,能够找到一个大于当前序列的新序列,且变大的幅度尽可能小。具体地:
- 我们需要将一个左边的「较小数」与一个右边的「较大数」交换,以能够让当前排列变大,从而得到下一个排列。
- 同时我们要让这个「较小数」尽量靠右,而「较大数」尽可能小。当交换完成后,「较大数」右边的数需要按照升序重新排列。这样可以在保证新排列大于原来排列的情况下,使变大的幅度尽可能小。
以排列 [4,5,2,6,3,1] 为例:
- 我们能找到的符合条件的一对「较小数」与「较大数」的组合为 2 与 3,满足「较小数」尽量靠右,而「较大数」尽可能小。
- 当我们完成交换后排列变为 [4,5,3,6,2,1],此时我们可以重排「较小数」右边的序列,序列变为 [4,5,3,1,2,6]。
具体地,我们这样描述该算法,对于长度为 n 的排列 a:
-
首先从后向前查找第一个顺序对 (i,i+1),满足 a[i]<a[i+1]。这样「较小数」即为 a[i]。此时 [i+1,n) 必然是下降序列。
-
如果找到了顺序对,那么在区间 [i+1,n) 中从后向前查找第一个元素 jjj 满足 a[i]<a[j]。这样「较大数」即为 a[j]。
-
交换 a[i] 与 a[j],此时可以证明区间 [i+1,n) 必为降序。我们可以直接使用双指针反转区间 [i+1,n) 使其变为升序,而无需对该区间进行排序。
作者:力扣官方题解
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
最小覆盖子串
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:“BANC”
解释:最小覆盖子串 “BANC” 包含来自字符串 t 的 ‘A’、‘B’ 和 ‘C’。
滑动窗口,用 unordered_map 存出现次数,全<0 就代表覆盖完了,从左到右遍历,先往右增长滑动窗口,覆盖完了左边收缩,没覆盖上继续往右增长,如此反复。取最小值即可。
最长有效括号
维护一个 cnt,从前向后扫一遍,cnt==0 就记录一下最长距离,<0 就从这个下标开始统计。
这样扫一遍无法统计到"(((())"这种情况,所以再从后往前扫一遍。
时间:,空间:
字符串相乘
可以用一个 int 数组存各位相乘之和,最后再遍历一遍进行进位。
时间:,空间:
FFT
多项式相乘最优,但不学。
时间:,空间:不明
寻找峰值
即用 logN 的方法寻找局部最大值,有点意思。
二分法,nums[i+1]>nums[i]则往 i+1 的方向走,start=i+1,反之往 i-1 的方向走,end=i-1。题目条件是 i 旁边两个数和 i 绝不相等所以可以这么干。
按上述方法“爬山”,可以确保在下一个区间里绝对存在一个峰值,所以只需要继续缩小区间就好了,因为数字随机,所以只能用 logN 的二分缩小区间。
时间:O(logN),空间:
移动零
将所有
0移动到数组的末尾,同时保持非零元素的相对顺序。
维护一个双指针,从起点出发,想象一个 0 序列不断蠕动,不断将非 0 的元素交换至身后并合并 0 让自己更长,最终头部到达终点即可。
颜色分类
排序 0,1,2
与移动零有一定相似性。遍历一遍数组,遇 0 放开头,遇 2 放尾,维护一个双指针。由于存在换过来还是 0 和 2 的可能性,所以对每一个当前数字,加一个 while 循环直到遇到 1。
时间:,空间:
最长重复子数组
DP,本来以为是 kmp 算法,结果是 dp。实际上子字符串匹配也确实可以用 dp 达到 ,但显然 kmp 会更优。
时间:,空间:
最长连续序列
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
哈希表存所有数,朴实无华。
时间:,空间:
翻转字符串里的单词
先反转整个字符串,再反转每个单词即可。
CC++#43;C++#43; 可原地反转,Java、Py、Go 不行。
时间:,空间:
最大正方形、统计全为 1 的正方形子矩阵
DP
代表处最长的正方形边长(同时也等于算上后新增的子矩阵数量,即以为右下角,一层一层往左上外扩,新增的子矩阵数量正方形边长)。
转移方程为,即 左/左上/上 最小值 +1。
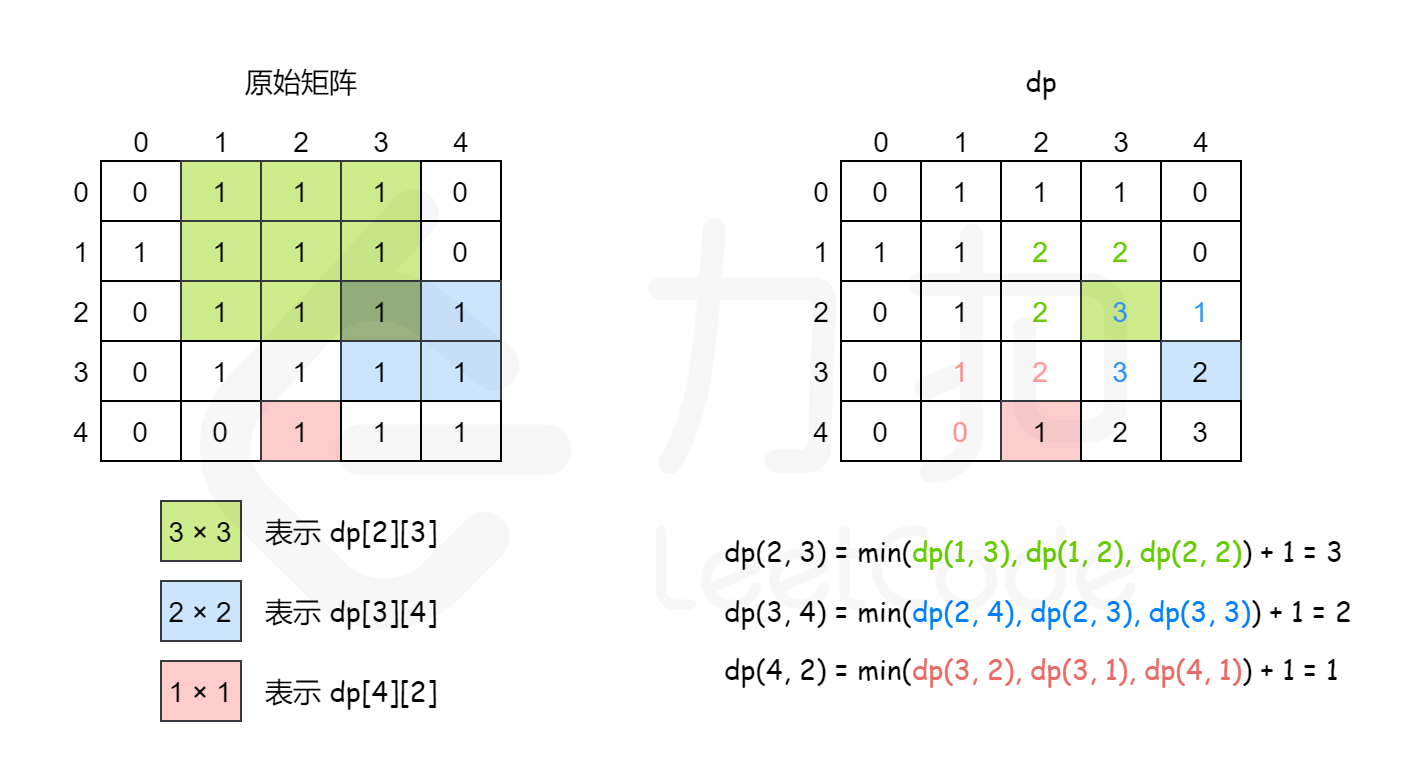
所以,最大正方形,子矩形总数。
删除一次得到子数组最大和
联系 最大子序和 一起看。本题是允许子数组删除一个负数,求这时的子数组最大和。
同样的,一维 DP 做不到,所以使用二维 DP。dp[i][0]与一维 DP 时一致,dp[i][1]代表删除一次的总和 max,其中,dp[0][1]无意义,可取 0。
这意味着要么是[0,i-1]删除了某个数的总和 max,要么是删除了 nums[i]的总和 max。易知:
此时,子数组最大和需要比较 dp[i][0]和 dp[i][1]取得。
时间:,空间:
打家劫舍
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12。
由于笔者先看的 删除一次得到子数组最大和 ,可以想到使用二维 DP,dp[i][0]代表打劫 i 家的总和 max,dp[i][1]代表不打劫 i 家的总和 max。
那么显然有,。
显然这个与上面的一维 DP 等价,并且也可以压缩成的空间复杂度。
时间:,空间:
航班预定统计
差分数组
时间:,空间:
美丽塔 II
两个数组的交集
哈希存出现过的(时间省一点)
时间:,空间:
排序 + 遍历(空间省一点)
时间:,空间:
找出游戏的获胜者(约瑟夫环)
只出现一次的数字
其他数字都出现两次,只有一个数字只出现一次
位运算异或,成对的数字都将被消除,剩下的就是答案。
时间:,空间:
随机链表的复制
与对象的深拷贝行为一致,是有意思的算法。
遍历三遍链表:
- 第一遍复制节点并插入这个节点的后面
- 第二遍将复制节点指向原链表节点的指针指向该节点的复制节点(即原链表节点的后一个节点)
- 第三遍分离复制链表和原链表
时间:,空间:
对称二叉树
使用递归函数,检查左右子树是否相等。
1 | class Solution { |
时间:,空间: