GSOC2024 Proposal-cn

如图所示：
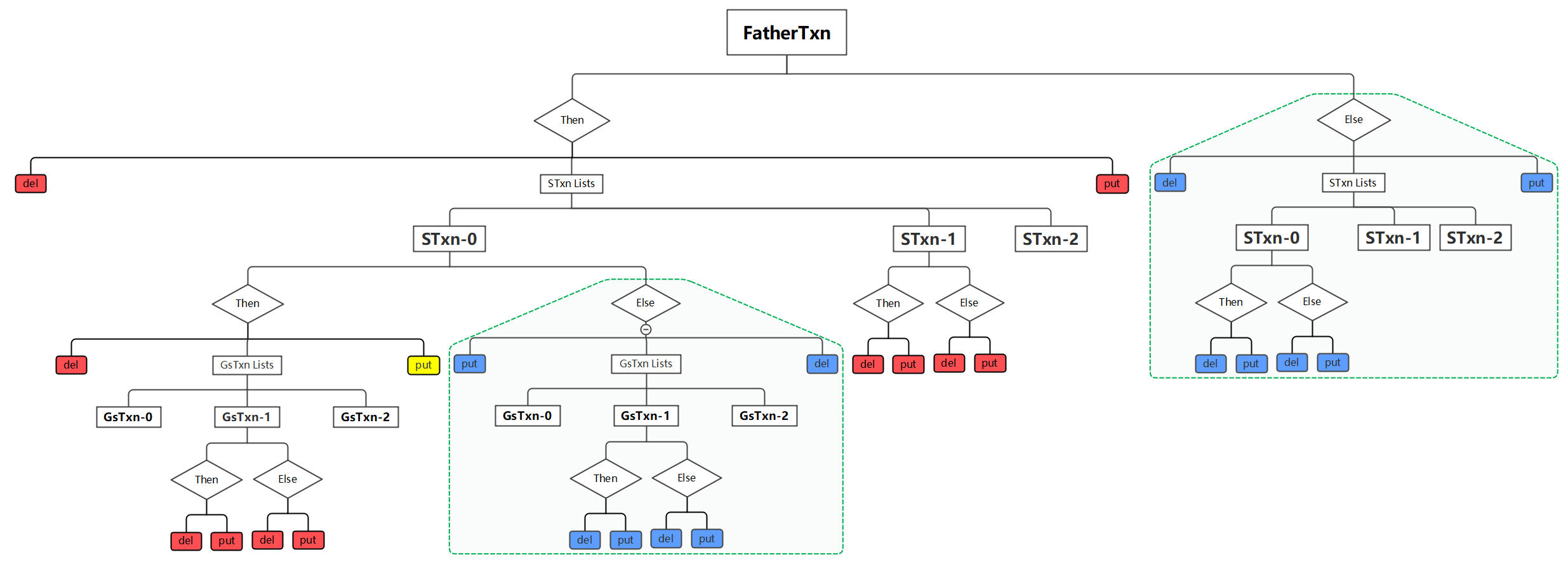
Overlapping rules

考虑STxn-0的put操作（注意，这里的put并不包括STxn-0的子事务如GsTxn-*的put操作），它不应该与图中标为红色的del与put相交，同时，它又可以与图中标为蓝色的del与put相交（换言之，这些背景是绿色的区域需要被排除）。这是因为Then和Else的语义注定了这两个分支只会选择一个执行，所以即使它们重叠了也无所谓。

方案一

首先考虑put与del相交的问题：

最好的办法莫过于构筑一棵包含了所有的del的区间树，然后遍历put进行查询。但如上所说，有一些del是需要被排除的，若是只存区间而不存事务间的父子兄弟关系，这将无法识别该排除什么。考虑到 Xline 作为一个 metadata 数据库，他的事务不应该有很多的嵌套结构以及很多的子事务，使用额外空间存一些信息是应当被允许的。

上面那张图有些复杂，实际上put与del的父子兄弟关系可以简化如下图：
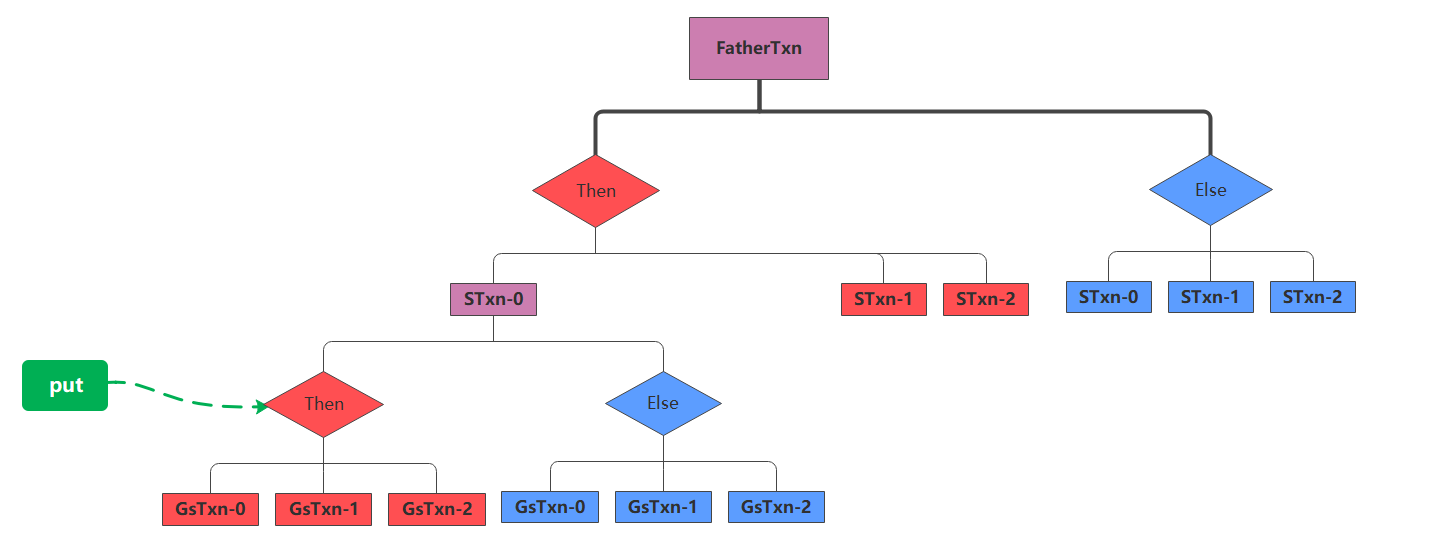
Overlapping Rules Simplified

考虑属于STxn-0的Then分支的put，它仍然不能与红色区域内的del相交，但可以与蓝色区域的del相交。

笔者需要解释一下为什么可以这么简化：

目前只考虑del，因此，其他的put就可以先隐藏掉，同时*Txn List也可以省略掉了
Then与Else本身包含del，因此它们会有颜色
而对于GsTxn-*这类事务节点，由于无论是它们的Then分支还是Else分支，要么全可以，要么全不可以与put相交，因此它们可以直接涂成红/蓝色
紫色节点只是笔者为了画面和谐涂上去的，因为红+蓝=紫。也代表该节点的Then和Else需要分开处理

那么显然这就是一颗多叉树。先考虑直接对其进行编码。比如，以节点在其父节点的Txn List的顺序依次编号0,1,2...，然后Then和Else分别为0和1。对于属于STxn-0的Then分支的put来说，它的编码就是00 00，而对于属于FatherTxn-Then-(STxn-0)-Else-(GsTxn-1)-Then的del来说，它的编码就是00 01 10。

举几个具体的例子：

对于编码为00 00的put，其应当排除的编码集合是[01 *, 00 01 *]，其中*代表任意编码。
对于编码为01 20 11的put，其应当排除的编码集合是[00 *, 01 21 *, 01 20 10 *]。

那么完全可以总结出一条规则：求put与del的 LCA 节点，该节点若是*Txn*这类节点，则put与del不相交；若是Then或者Else节点，那么put与del相交。

再进一步，考虑建一颗多叉树，FatherTxn作为root节点， $depth=0$ 。则易知：当 LCA 节点的 $depth\%2==0$ 时，则put与del不相交；当 $depth\%2==1$ 时，那么put与del相交。

那么判断put与del相交的步骤就可以确定了，如下：

构建一棵全局的区间树数据结构。这个数据结构应有以下的性质：
- 该区间树可以存（Range，Value）二元组，Value 可以是多叉树的路径编码，也可以是一个多叉树节点的引用
- 该区间树插入（RangeA，Value1）和（RangeA，Value2）两个区间后，查询的时候应返回[Value1,Value2]两个值，因为不同子事务之间可能会有一模一样的区间，这两个区间的编码信息不应该被覆盖。
开始递归的遍历各个子事务的各分支的put数组。对于每个put，查询del区间树，遍历查询到的区间集合根据上述的 LCA 或路径编码进行重叠检测。

现在考虑put之间相交的问题：

对于put来说，由于它是一堆点的集合，用 hashmap 构建重叠检测会更快一些。而且它们不需要担心顺序问题，完全可以在判断put和del相交的第二步，即递归遍历put数组的时候一起进行。

方案二

若是想少一些空间复杂度，应当有很多方法。比如，在递归地收集del的过程中，考虑直接进行重叠检测，笔者的简要思路如下：

若是递归遍历到最底层的*Txn*。应确保它的Then和Else分支一定可以通过重叠检测，然后将这两个分支的del和put合成一个del和put
然后两两比较与该*Txn*的处于同一级的其他*Txn*的del和put，注意到，这些*Txn*又处于它们父事务的Then或Else分支，因此可以跳回 1

细节不再阐述，像这样做的话，由于单独处理了Then和Else分支，所以不再需要记录这些事务的父子兄弟关系。

方案优劣比较

这两个方案用了很经典的时空复杂度互换的思想。

方案一增加了额外的空间复杂度，大致计算就是多用了 $8*Num_{del}$ 字节， $Num_{del}$ 是del中所有区间的总数。假如想更快一点，可以再建一颗子节点指向父节点以及记录了 $depth$ 信息的多叉树。
方案二不希望记录这些关系，结果就是时间复杂度的增加。对于每个*Txn*，它需要首先对自己的del建一颗区间树，然后要合并它所有子事务创建的区间树。而且，当它两两比较同级的del时，本质上是在 $n$ 棵小区间树上搜索，时间复杂度也会大于在一颗包含所有del的大区间树上搜索的时间复杂度。

笔者更倾向于使用第一种方案。因为 Xline 是一个 metadata 数据库，如前所述，他们不应该有很复杂的事务结构。方案一的空间复杂度实际由事务总数和del总数决定，del总数还可以通过区间合并减少一些。所以它的空间复杂度在可控的范围。

考虑方案一的极端情况下（实际上也是区间树的极端情况），遍历put一个值时查询到了非常多的del区间，无论最终重没重叠，这时都要一个一个的遍历这些区间判断是否重叠，即使区间树查询是 $logN$ 的时间复杂度，整个流程的时间复杂度此时会无限趋于 $N$ 。方案二则不会有这种情况，它单独处理了Then和Else分支，对于两两比较的场景，只要查询到任意区间，这都意味着重叠发生，可以返回DuplicatedKeyError了。

但是 Xline 仍然是一个 metadata 数据库，要是出现这种极端情况，笔者认为这应当是事务创建者的问题，而非 Xline 需要处理好的事。